"Teaching" Learner Dispositions

From my research I've learned

You

Can't 

Teach

Learner 

Dispositions.

Dispositions are a person's inherent qualities of mind or character.  

So in my mind this means they have to be developed.

And then adopted by each individual to employ at various times in their lives.

The research says we can teach techniques that lend themselves to learner dispositions. 

For example, we want our learners to persevere.

Teaching techniques of what learners can do when they get stuck 

Will help develop this disposition.

As we started this second semester,

I knew I wanted my classes to engage in the Painted Cube problem for two reasons:

1) Class schedules change at semester, so this non-curricular task would do the trick to get students working/thinking in random groups with new-to-them "class family members". 

2) I wanted to stay behind the scenes, hopefully collecting evidence of the six Learner Dispositions our staff had chosen for our school back in the fall.  

Speaking of the fall, we had worked hard at creating a BTC classroom where thinking, mistakes, and talking about the math pushed our learning.  So now that we had our learner dispositions identified for our Visible Learning journey, I was curious what our baseline data would show.

I was not disappointed!

All six learner dispositions were evident at times.

Not 100% of the time.

And not with every student.

But there were glimpses of each.

And I decided that's where I would start.

A resilient learner embraces challenges and perseveres. (Effect Size 0.56)

My students showed persistence in this low-floor high-ceiling task.  

Once they solved the 3x3x3 cube, I challenged them to find the solutions for the 4x4x4 cube.

100% of the groups stepped up to the task!

One student, one that does not seem to struggle much, simply quite when I suggested the larger cube,

Stating...since I didn't have a physical model or a picture for her to look at, she simply couldn't do it.

What to do?

I had seen teams draw a 4x4 and 4x4x4 models on their boards to get into the problem. 

But I didn't want to suggest that.

I wanted her to find a strategy to persevere.

As the rest of her group started chatting what they could do,

As she sat alone at a table,

I simply stated that I was surprised that she was the only student that day to quit so easily.

I reminded her that she could look at others' boards to get some ideas to help her move forward,

And then I walked away. 

As other groups solved the 4x4x4 and then ASKED if they could work on a 5x5x5 (making their own challenges),

I glanced back at my student whom I had left sitting at a table.

She was up at the board with her group sharing her ideas of how to move forward.

Perseverance.

Below are some of the comments I heard that relates to this disposition.

"First of all, I think we need to do this..."

"Let's try this..."

Team goes back to look at the physical model.

Team asks clarifying questions.

A curious learner wonders and wants to know more.

"Can we do a 5x5x5 cube now?"

Curious learners want to know more.

It is possible they were started to find some patterns/relationships in their work,

And were wanted to test it out with the next bigger cube.

This is exactly what I want my learners to do!

A reflective learner continuously thinks about, examines the results, and makes adjustments to their learning. (Effect Size 0.75)

This was the disposition I ended up being the most surprised about.

I never really thought my students were reflective learners.

Too many times I see students in my classroom come up with an answer and just accept it.

They throw out answers without any thinking behind it.

It seems like their goal is just to get it done at times.

So when I looked back at the data I had collected, 

my heart swelled that we were indeed on the right track.

Somewhere, this disposition had had seeds planted.

Was it in my questioning as I surveyed the work on their boards

That helped create this reflective nature?

"How do you know that's correct?"

"Tell me about your answer."

"Is that a correct solution?"

My data on the reflective learner.

"Wait...this should equal 27 [for the 27 total cubes]"

"This doesn't make sense." (erases answer)

"Look, this can't be right."

"Does this make sense?"

"We're still missing something."

"Ok, now we have to find out..."

"How does this equal 6?"

All around me I was hearing students reflecting on their findings,

And then questioning it!

Which prompted justifications.

* insert teacher smile here *

A creative learner is expressive and explores different ways to solve problems.

I will be honest.

This was one disposition that I wasn't sure how it would look like in the math classroom.

How could students be creative in solving problems while they were learning it?

Again, this low-floor high-ceiling problem opened the door to usher in the creativity.

Do these students understand the problem?

An emphatic...YES!

Do these students have the tools to extend the problem?

Yup.

Creativity.

In the math classroom.

For.

The.

Win.

A risk taker steps out of their comfort zone and overcomes their fears to make and learn from mistakes

As mentioned in some of the previous dispositions,

I saw risk takers eagerly embrace the challenge of a larger cube.

But there is one risk taker that stands out in my mind.

Remember that this was day ONE with new class schedules.

Students were in classes with new faces.

And new classroom climates needed to be established.

There was one class where this was very apparent.

No. One. Spoke.

As I introduced the problem and asked what they noticed...

No. One. Spoke.

As I stated the questions a little differently to help with clarity...

No. One. Spoke.

Just as I was thinking we may need to employ the Think-Pair-Share strategy,

One of my more anxious, not-confident students, raised her hand to share.

This was my risk-taker poster child.

I knew just how much courage she had to muster up to move class along.

And finally,

A connected learner relates prior knowledge and/or real-world experiences to their learning.

Again, this was one that I wasn't sure if I would see it in the math classroom.

As I introduced the problem,

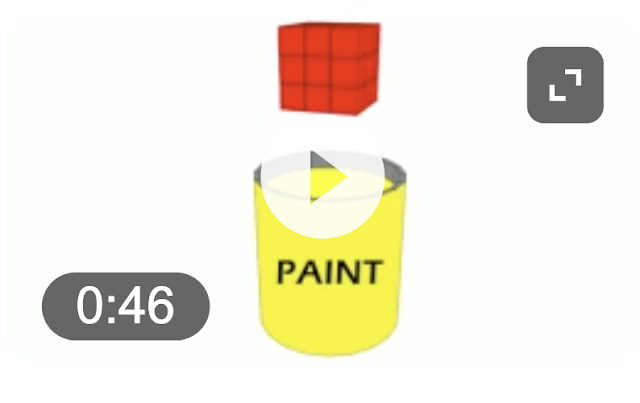
I simply showed them this picture...

And asked the question, 

"What do you think today's task will be?"

After they described what they believed the task would be,

Dunking the red cube into yellow paint,

I asked them what already knew about the problem.

Their answers amazed me.

While I was expecting statements about the task

or that the cube looked like a rubrics cube,

The answers I got were all connected to math they had already learned.

Cubes.

Area.

Surface Area.

Volume.

Faces.

And the conversation that ensued afterwards

Supported their understanding of each term 

As they contributed to the discussion.

So moving forward.

Where to next?

I will share these exact findings with the students.

I will have them contribute their thoughts on their learning

Using the open-ended rubric.

And then have them individually assess themselves using the ranking rubric.

In future lessons,

I will be sure to reinforce these dispositions 

With specific feedback as I see them utilized in our learning.

Not sure how to remove this!

When a Mistake Reflects the Research

I didn't mean for it to happen.

As I answered my students question, 

I had no foreshadowing 

of what was about to happen.

To fully understand where I'm going with this,

let me give you a brief snapshot of life in my classroom.

Learning in my classroom looks different.

Students are working at vertical white boards.

Students are writing their OWN notes from what they've LEARNED.

Students are asking specific questions to further their understanding.

Students are getting immediate feedback on their work 

by checking the answer keys posted around the room.

Students are not graded on anything except individual work

which is usually quizzes or projects.

Until this fateful day.

When we were learning angle vocabulary through an EdPuzzle video.

Which was to be done individually.

One student in 4th hour asked,

"Is this for a grade?"

I answered honestly that "yes, it was."

And then it quickly became clear.

Crystal clear.

Why assigning a grade on learning is actually detrimental to the learning.

I first noticed students talking to each other.

Comparing and changing answers.

Hands were going up.

Lots of hands.

Needing confirmation from me that they were getting questions correct.

There was no individual reflective comments like,

"Oh...that's what it is."

"Oops...what did I do?"

There was a sense of tension to finish.

To get the good grade.

The focus was no longer on the learning.

It was solely on the grade.  

A grade that wasn't even going to change anyone's grades.

But if this focus on grades was replacing the focus on the actual learning????

Then.

That.

Is.

A. 

Problem.

What a wonderful accident to have happen!

To showcase that learning can occur without attaching a number to it.

In fact, more learning occurs when the percentages are taken away.

In the past years when I've taken grades on everything, 

I usually have anywhere from 8-15 failing grades each year.

HOWEVER, the last three years when I've implemented Building Thinking Classrooms,

The numbers have dropped dramatically!

This year, I have only 2 students currently failing math.

Let's Talk About Flow

Both BTC and Visible Learning talk about flow.

This is that sweet spot in a lesson

Where students are being successful and challenged at the same time.

It's not too hard.

It's not too easy.

It's accessible.

But intriguing.

Just enough that pushes students forward,

Giving them confidence to keep going.

Today's first task was to demonstrate understanding from the day before.

Students solved a problem on an index card

And then on the back of the card

They communicated their struggles, questions, or what they hoped would be in the lesson today.

While I had a lesson ready to go,

This information gave me just what I needed to focus on.

As we worked through the problems,

Tackling the questions, the mistakes, and questions of the students,

Learning was moving them forward.

And pretty soon, in one class, students were asking for harder problems.

We had reached the point where the challenge was gone,

It was too easy now.

Unfortunately, I did not have other problems on the ready,

But quick thinking, allowed me to create a more challenging problem.

And as they worked this problem,

I quickly assembled a couple more that would push them.

The conversation that followed pushed thinking even more,

And pretty soon they were wanting another problem.

At the end of the hour, I gave them one that I knew they weren't quite ready for.

I prefaced it with this one was too hard,

And I doubted if anyone could solve it.

I would say about 80% of the class literally dove right in to prove me wrong.

Only a couple quit when they saw the problem.

But the silent pressure of their classmates working away got to them,

And pretty soon I saw them pick up their dry erase markers and start in.

How amazing is it to see the research play out first hand in the classroom!

When students are simply moving along in flow,

In the zone,

Where learning is visible,

As success is found,

And confidence is built

As the complexity grows.

Rubrics Making Learning Visible

Today we went over the quiz retake procedure.

We used the BTC rubric idea that I tailored a bit for our needs.

Students recorded their results for each question 

For the first two quizzes we took.

A checkmark for a correct answer.

An X for incorrect answers.

An S if it was a silly mistake.

And an N if the question was not attempted.

Students then analyzed the results

To find their strengths and weaknesses.

The areas to work on gave the students a visual of their learning

And what they need to focus on before the retake.

Observation

I was super impressed to see the focus for this activity.

But it didn't exactly surprise me.

This activity was directly related to their personal learning.

And they were taking it seriously!

Analyzing their own data happened naturally.

Students seemed to immediately focus on the X's.

Trying to figure out what they did wrong.

Students looked for areas of growth.

Students could see the progression of learning...

where they started and where the learning was going.

For example, a student noticed that they missed all the numeric expressions on the integer quiz,

But by the time we got to the Algebraic Representation quiz,

They realized they had gotten all those questions correct.

Growth. Had. Occurred.

And they were seeing it!

On their own!!!

Success.

Sharing Data

I also shared with the class the pre- and post-test data.  

And again, I was impressed with the conclusions they were making.

Sharing data that represents them is so important.

It puts an emphasis on learning.

On THEIR learning

On growth.

On THEIR growth.

Using Success Criteria to Help Students Visualize Their Learning

The Catalyst 

Word on the street was that the 8th graders were freaking out about the Algebraic Representation quiz coming up.

What great feedback for the teacher!

And what great feedback for the students!

This freaking out is exposing some learning gaps and students are paying attention!!!!!!

So today, we dove a little deeper to find out WHY the freaking out was happening.

The Plan

To start the lesson, I relied on the success criteria as my guiding factors.

I listed the success criteria on the board.

Along with another criteria "other".

This "other" category was used for students to share what other stresses they were feeling in this unit

(not listed in the success criteria)

or if they were feeling fairly confident, to just place a blank sticky note in this space.

So in summary, the goal was for students to reflect on where they were struggling

And place a sticky note...or two...to communicate this.

(Think...horizontal bar graph).

This immediately gave a visual for the focus of the lesson.

I had already created a Top Hat Organizer to address these concerns,

But knowing where the students wanted to concentrate,

Was a bonus in my book!

Student data chart for where the freak outs were happening.

Top Hat Organizer based on a question from the prior day about the difference 

between expressions and equations. The success criteria were also woven 

through the whole group discussion as we filled out the organizer. 

What Was Observed

Whoa.

I was not prepared for what was to come after the stickies had been placed.

As we worked on completing the Top Hat Organizer,

students asked specific questions,

aligned perfectly with the success criteria,

to help their understanding.

There was no, "I don't understand any of this!"

There was no, "This is hard!"

There was only questions when misunderstandings or confusion set it.

Clarifying questions.

Attempts to summarize their understanding.

Students had a handle on their learning

And could visualize where they were falling short!

The Results

After the short whole group lesson,

Students were able to practice.

Because this was their day to focus on what they needed,

I allowed them to choose between independent or small group work.

For some working independently to check their own understanding 

Would allow for more growth,

While for others, being able to talk about and work through with another would help them fill any gaps that still existed.

At the end of the class, 

Students were instructed to remove their sticky if they were feeling confident at this point for quiz.

If their sticky remained up there,

They could assign themselves homework tonight...

...finish the practice problems from today or complete another set of problems that I had ready to go...

to help study for the quiz tomorrow.

My Reflections

By starting the class with success criteria in this way,

I saw first hand how some other areas in the 10 Mindframes book are present in the classroom.

Feedback.  

What wonderful feedback for not only the teacher,

But also every individual student!

Gaps in the learning process are exposed to both entities,

Creating a need to learn to help fill that gap.

Learning made visual.

Nothing is more visual than a chart.

We use them all the time to analyze our growth.

Today, the students were an active part in creating the visual,

And seeing the benefits from concentrated efforts when learning.

Other Thoughts

One class did not follow the observations that I saw in the other four classes.

What was the difference?

One difference I noticed was when the stickies were placed on the board.

Comments were made by students as put downs for sticky note placement.

This created an atmosphere of distrust

Which essentially eroded the lesson that followed. 

The focus was not intrinsic anymore.

The effort was very lack luster.

With no one wanting to show that they cared about the learning.

We spent the first two full weeks working on creating a climate

Where mistakes are valued, sharing thoughts are encouraged, and work ethic is expected.

I will continue to reflect what I can do 

To help this class experience learning as the others do.  

Implementing Learning Targets and Success Criteria

Two weeks ago, our teaching staff spent two days 

entrenched in Visible Learning by John Hattie,

learning about learning targets and success criteria.

We learned what each was, 

how they were different,

but more importantly,

how they work together.

When teachers use learning targets and success criteria,

they find greater direction for their lessons.

By slowing down and really thinking about where they want to take the students,

teachers can develop learning targets and success criteria

that is not only clarity in the learning that is to happen,

but a wonderful visible map for their lesson.

A plan of sorts where all participants,

both teachers and students,

know WHERE (learning target) they are going 

and HOW (success criteria) they will get there.

So how did I incorporate these new ideas into my lessons?

First, I changed when I wrote my learning target.

Learning targets had always been a piece of my lesson planning.

Unlike in Visible Learning where the learning targets are thought through first,

I would usually plan my lessons (always knows WHERE I wanted to go with the lessons)

But then write the target at the end of the planning.

Now?

The Learning Target and the Success Criteria are the first things I get down on paper.

With being new at this, though,

I feel it is important to emphasize that even though I start with them,

it is a work in progress,

as I often reword them before I post for the class.

Next, I changed where I displayed the learning target with the success criteria.

Instead of across the top part of my white board,

in the format of "I can" _______ "in order to" __________

I now use a designated whiteboard.

With the words, "Learning Targets" and "Success Criteria" as my headings,

I can daily update our learning plan.

I use little checkboxes in front of my success criteria

As this is a great reminder for students that our goal is to check those off at the end of the lesson. 

With all the focus and chatter happening in our building

Surrounding these two concepts,

learning targets and success criteria began to be a daily focus in my classroom as well.

As I did previously, I would introduce our learning for the day by addressing the target.

Now I would add just how that target would look if we were successful in our endeavors.

But probably the most important thing I changed

Was that I would address the success criteria at the END of class.

This is really, in my opinion, where the strength of the success criteria lies.

Students need a little time to reflect on their learning.

Are they able to check off those boxes?

Here are a few ideas I've used these first couple weeks 

to bring success criteria back to the focus at the end of the lesson.

Review the success criteria together in class.  

     a) Students, in their minds, check off the boxes they feel like they were successful in.

     b) Students indicate with a thumbs up or thumbs down to give the teacher feedback for the next day's

         lesson.

     c) Students mark on a continuum their progress with the criteria

     d) Along with the continuum, the numbers 1-4 could be added for students to select where they are.

         These can be shared with the teacher through an exit ticket, giving feedback for the next lesson.

     e) An exit ticket problem so students can show their understanding.

     f) The teacher can observe student work to see where they are in their understanding.

     g) Have students write their own success criteria.  For example, after looking at their math scores from

          the previous year and our initial Fastbridge scores, students wrote their success criteria for how they

          will know when the year is done that they were successful in 8th grade math.

Clarification: All of these thoughts are based only on reading the book 10 Mindframes for Visible Learning, two days of professional development, collaboration between teachers, and most importantly, trying it out with my students.  

Stay tuned for a visual that shows the relationship between learning targets and success criteria!

Visible Learning Meets BTC - Ch. 11 - A Vision

As I finish this book,

I won't lie,

I am a little overwhelmed 

At how to incorporate all ten mindframes

In the spiderweb approach they introduce.

But then I think about where my teaching is at today,

How all my experiences, learning, professional developments, book reading, and conversations

Have led to honing my craft.

To get to the point where I am today,

I have taken an idea,

Implemented it,

Tweaked it,

Reflected on it,

Until it became a part of my skill set.

One step at a time.

One day at a time.

One lesson at a time.

One mistake at a time.

One success at a time.

It's doable.

And I can't wait to see where this new journey takes my teaching!