You
Can't
Teach
Learner
Dispositions.
Dispositions are a person's inherent qualities of mind or character.
So in my mind this means they have to be developed.
And then adopted by each individual to employ at various times in their lives.
The research says we can teach techniques that lend themselves to learner dispositions.
For example, we want our learners to persevere.
Teaching techniques of what learners can do when they get stuck
Will help develop this disposition.
As we started this second semester,
I knew I wanted my classes to engage in the Painted Cube problem for two reasons:
2) I wanted to stay behind the scenes, hopefully collecting evidence of the six Learner Dispositions our staff had chosen for our school back in the fall.
Speaking of the fall, we had worked hard at creating a BTC classroom where thinking, mistakes, and talking about the math pushed our learning. So now that we had our learner dispositions identified for our Visible Learning journey, I was curious what our baseline data would show.
I was not disappointed!
All six learner dispositions were evident at times.
Not 100% of the time.
And not with every student.
But there were glimpses of each.
And I decided that's where I would start.
A resilient learner embraces challenges and perseveres. (Effect Size 0.56)
My students showed persistence in this low-floor high-ceiling task.
Once they solved the 3x3x3 cube, I challenged them to find the solutions for the 4x4x4 cube.
100% of the groups stepped up to the task!
One student, one that does not seem to struggle much, simply quite when I suggested the larger cube,
Stating...since I didn't have a physical model or a picture for her to look at, she simply couldn't do it.
What to do?
I had seen teams draw a 4x4 and 4x4x4 models on their boards to get into the problem.
But I didn't want to suggest that.
I wanted her to find a strategy to persevere.
As the rest of her group started chatting what they could do,
As she sat alone at a table,
I simply stated that I was surprised that she was the only student that day to quit so easily.
I reminded her that she could look at others' boards to get some ideas to help her move forward,
And then I walked away.
As other groups solved the 4x4x4 and then ASKED if they could work on a 5x5x5 (making their own challenges),
I glanced back at my student whom I had left sitting at a table.
She was up at the board with her group sharing her ideas of how to move forward.
Perseverance.
Below are some of the comments I heard that relates to this disposition.
"First of all, I think we need to do this..."
"Let's try this..."
Team goes back to look at the physical model.
Team asks clarifying questions.
A curious learner wonders and wants to know more.
"Can we do a 5x5x5 cube now?"
Curious learners want to know more.
It is possible they were started to find some patterns/relationships in their work,
And were wanted to test it out with the next bigger cube.
This is exactly what I want my learners to do!
A reflective learner continuously thinks about, examines the results, and makes adjustments to their learning. (Effect Size 0.75)
This was the disposition I ended up being the most surprised about.
I never really thought my students were reflective learners.
Too many times I see students in my classroom come up with an answer and just accept it.
They throw out answers without any thinking behind it.
It seems like their goal is just to get it done at times.
So when I looked back at the data I had collected,
my heart swelled that we were indeed on the right track.
Somewhere, this disposition had had seeds planted.
Was it in my questioning as I surveyed the work on their boards
That helped create this reflective nature?
"How do you know that's correct?"
"Tell me about your answer."
"Is that a correct solution?"
My data on the reflective learner.
"Wait...this should equal 27 [for the 27 total cubes]"
"This doesn't make sense." (erases answer)
"Look, this can't be right."
"Does this make sense?"
"We're still missing something."
"Ok, now we have to find out..."
"How does this equal 6?"
All around me I was hearing students reflecting on their findings,
And then questioning it!
Which prompted justifications.
* insert teacher smile here *
A creative learner is expressive and explores different ways to solve problems.
I will be honest.
This was one disposition that I wasn't sure how it would look like in the math classroom.
How could students be creative in solving problems while they were learning it?
Again, this low-floor high-ceiling problem opened the door to usher in the creativity.
Do these students understand the problem?
An emphatic...YES!
Do these students have the tools to extend the problem?
Yup.
Creativity.
In the math classroom.
For.
The.
Win.
A risk taker steps out of their comfort zone and overcomes their fears to make and learn from mistakes
As mentioned in some of the previous dispositions,
I saw risk takers eagerly embrace the challenge of a larger cube.
But there is one risk taker that stands out in my mind.
Remember that this was day ONE with new class schedules.
Students were in classes with new faces.
And new classroom climates needed to be established.
There was one class where this was very apparent.
No. One. Spoke.
As I introduced the problem and asked what they noticed...
No. One. Spoke.
As I stated the questions a little differently to help with clarity...
No. One. Spoke.
Just as I was thinking we may need to employ the Think-Pair-Share strategy,
One of my more anxious, not-confident students, raised her hand to share.
This was my risk-taker poster child.
I knew just how much courage she had to muster up to move class along.
And finally,
A connected learner relates prior knowledge and/or real-world experiences to their learning.
Again, this was one that I wasn't sure if I would see it in the math classroom.
As I introduced the problem,
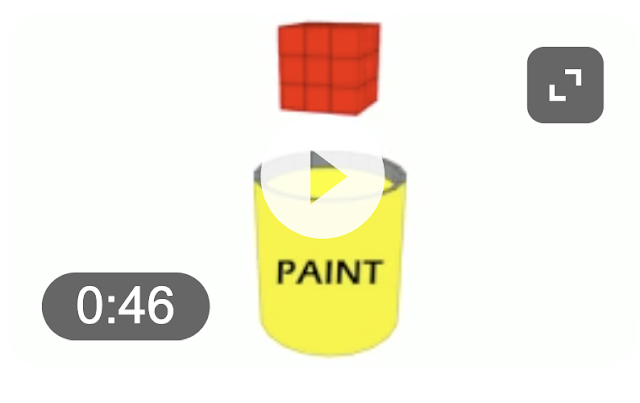
I simply showed them this picture...
And asked the question,
"What do you think today's task will be?"
After they described what they believed the task would be,Dunking the red cube into yellow paint,
I asked them what already knew about the problem.
Their answers amazed me.
While I was expecting statements about the task
or that the cube looked like a rubrics cube,
The answers I got were all connected to math they had already learned.
Cubes.
Area.
Surface Area.
Volume.
Faces.
And the conversation that ensued afterwards
Supported their understanding of each term
As they contributed to the discussion.
So moving forward.
Where to next?
I will share these exact findings with the students.
I will have them contribute their thoughts on their learning
Using the open-ended rubric.
And then have them individually assess themselves using the ranking rubric.
In future lessons,
I will be sure to reinforce these dispositions
With specific feedback as I see them utilized in our learning.
Not sure how to remove this!











No comments:
Post a Comment