Rough Draft Math by Amanda Jansen.
I saw somewhere that this book is a good choice to follow Building Thinking Classrooms.
I'm one chapter in,
And I believe I have made a good choice!
Some highlights...
"By expressing ourselves, we learn more..."
"getting into the conversation, helps you understand..."
"participating in math class is an opportunity to continue learning, not an obligation to perform..."
"When we learn, we actively work to make sense of an idea that does not make sense to us yet."
"Our use of bumpy language is actually productive struggle in action."
"Rough draft thinking sounds like communicating what we notice, explaining why something does or does not make sense initially, trying on a new way of seeing a relationship, or making new connections and articulating them".
This first chapter brought to mind several things that happened in my classroom this week.
Rough Draft Math might not be so hard to implement as the next step.
Scenario #1
While reviewing slope, one of my questions referred to parallel slopes.
A couple questions later, it focused on a slope less steep that y=1/2x+8.
A student suggested using -2 as the new slope.
After graphing the two slopes,
A student just blurted out, "Those lines look like they cross at a 90 degree angle."
This prompted a discussion on what the mathematical vocabulary is for two lines that intersect at 90 degrees.
Which then moved the discussion forward to a place I had never anticipated going...
Teaching what slopes make perpendicular lines.
I wrote on the board that a line with a slope of 1/2 is perpendicular to a line with a slope of -2.
I then made a quick decision to offer some thin-slicing problems to see if students could make sense
of what slopes make perpendicular!
Students quickly talked through the first couple of problems,
If a line has a slope of 1/3, the slope of a line perpendicular to it would be ____
If a line has a slope of 1/4, the slope of a line perpendicular to it would be ____
I then asked if they could put into words what they saw was happening.
Many students yelled out, "Keep Change Flip!"
I could see why they said this, they were seeing fractions flippling and the sign was switching from positive to negative in the examples I had given.
With several wondering question from myself,
"What are these fractions called when the numerator switches places with the denominator?"
"What do you mean by 'change'?"
"What's a better word for when a number goes from positive to negative?"
And pretty soon we got it summarized that perpendicular lines have slopes that are opposite reciprocals.
"participating in math class is an opportunity to continue learning, not an obligation to perform..."
"getting into the conversation, helps you understand..."
I had students in the conversation that rarely jump in.
Some students were leaning forward in anticipation of figuring this out.
It was one of those moments in math where you just let the conversation take over.
Scenario #2
"Rough draft thinking sounds like communicating what we notice, explaining why something does or does not make sense initially, trying on a new way of seeing a relationship, or making new connections and articulating them".
On 2/22/22 students could choose from two activities...
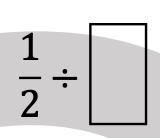
One activity was working with fractions.
They had to make all the problems equal to 2.
It was eye-opening for me to see their number sense and how they thought and worked with fractions.
Of course, dividing fractions, seemed to be the biggest stumbling block.
As I listened to students trying to make sense of these problems,
I wondered how we could make this process easier with pictures.
After deciding to go with the concept of pizzas,
We talked through it together as a class, myself included,
How to visualize these problems to figure out how to get the solution of 2.
Ironically, while typing this, I now have noticed another relationship that would have made this so much easier.
We could easily have just divided it by two to find the divisor we needed!
An example of where there wasn't enough time to finish the conversation!
"When we learn, we actively work to make sense of an idea that does not make sense to us yet."


No comments:
Post a Comment