Thoughts on Thin Slicing

We have been thin-slicing our way through these first couple months!

Started with adding and subtracting integers,

And had students begging for harder problems. 

Brought in fractions,

And NO ONE BATTED AN EYE.

What?

No groans?

No freak outs when I mentioned the "f" word????

Who are these people????

Moved on to algebraic equations.

Thin-slicing for writing algebraic equations.

Thin-slicing for solving algebraic equations with like terms.

Thin-slicing for solving algebraic equations with variables on both sides.

Thin-slicing for solving algebraic equations with the distributive property.

It's amazing the material we can cover and master in a much shorter time!

My only dilemma?

All. The. Talking.

The extra talking.

The non-task talking.

I've tried various approaches.

One problem at a time announced verbally for all the groups works until I find myself having to talk over them.

Handing out problems has me running around the room like Hammie from over the Hedge.

What seems to work the best is posting the problems (listed from easy to more complex) along with the answers.

Students can answer at their own pace.

Check their work.

And move on.

I can work the room.

Correcting misconceptions as I see them.

In my books, this seems to be a win-win situation for all.

But with variety being the spice of life,

I will try to mix it up a bit

So we don't get bored with the same ol' routine.

My thoughts for today.

It's Friday.

We made it through another week.

And I am tired.

But not as tired as I could be if I weren't using the BTC approach in my classroom!  :)

The Power of Choice

For today's lesson, I offered the students a choice in the problems they solved.

We talked about closing our gaps,

With one of our gaps being fractions.

We also talked about where our lesson ended yesterday,

Solving operations with integers.

Today's assignment held problems with positive and negative fractions

As well as some fun integer puzzles.

Every small group chose to start with the fraction problems.

People.

In all of my years,

Students will shy away from fraction problems.

They will groan.

They will throw fits.

They will refuse.

Today...

They chose fractions.

#smallwin!

The Locker Problem Takeaway

Today was the Locker Problem.

Our last non-curricular task.

My takeaway?

Students need to feel comfortable taking a large problem and making it smaller.

Most of my groups concentrated on how to display the 100 lockers.

This slowed down their thinking progress.

During consolidation, we looked at how our brains work better with a smaller snapshot of the problem.

Which, in the long run, can. ultimately get us to the answer!  :)

Ch 10 Reflection: Consolidate a Lesson

This is probably my favorite part of BTC.

Bringing the discussion full circle. 

The one thing that stuck with me though,

Was to level to the bottom.

How many times did I level to the top,

The place where we all needed to get to,

Only to have it flop, with everyone feeling frustrated.

By starting with the bottom of the tiered problems,

The ones that everyone successfully solved,

We were able to get everyone on the same page,

And then could slowly work our way through the more challenging ones...

And get more students where we needed to go in the process!

One thing that I need to work on is keeping the students standing next to their boards.

I started to have students sit back down at their tables, but according to the research, this drastically diminished the thinking.

Gallery walks.

I tried these.

What I learned is that I need to have a specific goal for the walk.

What specifically should they be looking for?

Are they comparing methods to find similarities?

Are they looking for differences?

Are they trying to find misconceptions or mistakes?

Something to work on this year!

Ch 9 Reflection - Hints and Extensions

"If we are thinking, we will be engaged."
"If we are engaged, we are thinking."

This is my goal.

Every lesson.

Facilitating this optimal experience can get a little tricky though at times.

Especially when frustration sets in.

Either on my part or the students.

Three things to remember when aiming for an optimal learning experience.

1) Clear goals

2) Immediate feedback

3) A balance between the ability of the doer and the challenge of the task

Creating clear goals seemed to get better each time.

I learned quickly where loopholes would be found

And addressed those head on as we headed into a task.

Immediate feedback was sometimes right on point

And sometimes left me feeling like I was playing whack-a-mole.

I soon realized that when I was found running around the classroom

In a state of total frustration,

It was actually because the task I had selected was not balanced between the ability and challenge level for the student.

As I got better with creating thin slicing learning activities,

I started to see the magic happen.  

Not only were students being more successful

Because the challenge was very small between each task,

The frustration levels decreased dramatically.

And then a wonderful moment would appear that would take me by surprise.

STUDENTS WANTED A HARDER PROBLEM!

The excitement at being able to solve more difficult problems was amazing!

You could hear it.

You could see it.

And I, as the teacher, just revelled in the moment.

This is what I had been seeking.

My goal for this next year is to create more thin slicing opportunities.

For some concepts, it's super easy.

For others, it takes more time to set up a series of problems.

I conducted the thin-slicing lessons usually two different ways.

Sometimes, I would have the problems written out on cards,

And as students completed one, I would hand them another as I made my rounds.

This was beneficial as I could address mistakes and misconceptions for each small group

Without having to drag the entire group into the discussion.

Groups could keep working at their own pace,

Slowing down only when they started to struggle.

Other times, each group worked the same problem at the same time.

This allowed for quick little popcorn whole group discussions as we compared the boards

Before starting on the next problem.

Ch. 8 Reflection...Student Autonomy

Students were soooooo used to going to the teacher when things got challenging.

They didn't trust themselves.

They didn't trust their classmates.

But it all boiled down to one thing...

They didn't want to take the time to think.

Couple that with the teaching of not copying from others,

And students seemed at a loss of how to move forward.

Many class discussions had to be had

On what using others' thinking looked like,

What it meant,

And ultimately, how it could be helpful for everyone's learning!

We talked about the benefits of looking at other boards when the going got tough.

How was this helpful?

Students could find validation in what they were trying.

Students could discover multiple methods they may not have thought about.

Students could compare solutions or strategies

Which would then prompt more thinking on who was correct and where was the mistake.

One thing I need to work on,

Is how to use student autonomy to keep the problems flowing. 

Students are quick to erase once they have solve a solution.

It would be beneficial,

Especially during thin slicing problems,

That seem to be solved at a greater rate of speed,

To always keep the previous problem up on the board,

To allow for other groups to see the problem and keep moving.

To do this...

1) Have the problems numbered for easy reference between boards

2) Students MUST write down the problem before trying to solve to help communicate with other boards that are needing to move on.

3) Encourage just copying the problem and start solving on their own before assessing how the answer was derived.

Ch. 7 Homework Reflection

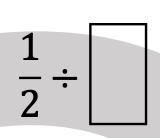
Aside from the white boards propped all around my room,

The change in how homework was handled was probably the biggest change.

Pre-covid I would take completion grades on practice.

Students were to "complete" the practice before we moved on.

After reading this book, it became crystal clear how this completion was happening.

Students were completing it JUST TO HAVE IT DONE.

The purpose of practicing and becoming more efficient in the new skills

Was not even on their radar.  

Simply getting it done, whether by copying another's work or just putting reasonable answers,

Was acceptable in their eyes

And MILES away from the purpose I had in mind.

During hybrid and remote learning,

I quickly realized that I had to take a grade on every little thing mentioned in Google Classroom.

It didn't take long to realize that the math grade was reflecting work ethic and responsibility

Instead of any true understanding of the concepts.

And then along comes BTC!

No more grades for any learning that occurs in the classroom.

Whether at the boards or in Check Your Understanding situations,

Students did as many problems as they wanted,

Knowing that any problems not completed would be good practice for learning the concepts.

But it was not required.

The focus quickly shifted to understanding the material 

And away from having to complete all the problems.

We talked a lot about how many problems were needed to learn and apply a new skill,

And how this number could fluctuate from person to person,

And from concept to concept.

Another change was the availability of the answer sheets.

For every Check Your Understanding, answer keys were posted around the room.

Students could check their work as often as they liked.

The questions prompted from this approach were much more specific

And the amount of thinking during this activity was increased immensely.

It was interesting when new students would join our class.

When these students realized the answers were there for their taking,

They became very excited...anticipating the ease of completing the assignment.

When they eagerly asked if they could copy the answers,

And when I answered, "Sure!  Go ahead!"

My students were quick to clarify that copying would not help them understand the math.

And then when it came time for the quiz where they could show off what they learned,

The person copying the answers would have a hard time!

Oh how I loved this shift in thinking!!!

My only conundrum with all this centers around the Simulation Trainer in my math curriculum.

The simulation trainer is totally a mimicking activity.

And as the book points out, "mimicking has limitations and is antithetical to the kind of thinking behaviors that thinking classrooms are trying to foster".

To incorporate both ideas, we use the Data/Computation problem at the boards.

And then the simulation trainer is done individually as a Check Your Understanding of sorts.

After every problem, is a video of how to solve it.

Repetition.

But I will be honest,

I do see thinking decrease during this time.

I will have to keep thinking how I can best use this component in a BTC classroom.

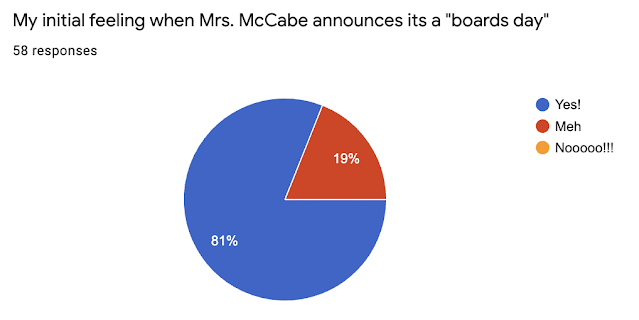
By the end of the year, students were reporting that they liked this "new" way of grading.

66% of the students liked it.

28% of the students had no opinion either way.

Only 7% did not like it, stating that they would like other opportunities to improve their grade.

Some of their comments to explain why they liked (or didn't like) about grades not being taken for class learning.

"It made me more relaxed and confident about this class and made me feel better about making mistakes."

"It allows me to make mistakes and learn from them and not get a bad grade because I didn't understand it."

"I loved how I could just learn so much and write it down and not have to get graded on it till the test. I believe it really helped me succeed in your class."

"It's learning. It shouldn't be graded."

"Because then people were working slow and not fast."

"It made my grades stay high and it made it seemed easier and less stressful."

"It makes the class seem like less of a thing we have to attend and something we WANT to attend."

When asked how they used the answer keys...

88% used them to check their work

76% corrected any mistakes they made

66% used the answer to help them figure out the problem

I loved it as well as the grade finally reflected true math understanding.

The number of semester F's fell considerably this year with only 1 semester F in the fall.

Last year we had a total of 9 F's for the entire year

And during that crazy hybrid/remote year??? 15 F's!  

Ch. 6 Giving Tasks in a Thinking Classroom

Our math curriculum has a 7-10 minute review called Test Trainer.

It is to be done at the beginning of each class period.

However, this year, I changed it to the last 10 minutes

So we could best utilize that first five minutes to get the task up and going.

Before this new curriculum and implementing Test Trainer,

I had always just jumped in to the lesson,

Somehow sensing before reading about the research that backs it up,

That engagement early on in the class period is optimal.

Just ask my principal...it's because of this mindset that I forget to take attendance!  

Oops!

Anyway, by pushing Test Trainer to the end of the day,

We noticed some positives and negatives.

The students liked it at the end, 

As they reported that their minds were already primed for math

And they thought it was reflected in how they did.

However, there were MANY times when Test Trainer just did not happen.

The problem or the whole group discussion took priority

As learning would reach its peak at about the time we should have been shutting down for TT.

At the beginning of the year, 

I did give the tasks outloud with the students standing around me.  

However, with this group,

Having them all in such close proximity,

The talking increased!

I tried various other ways...

Giving the instructions verbally while they sat in their table groups,

and giving verbal instructions after moving them to their boards.

Both had their downfalls.

At their table groups, they were still seated

And not as plugged in had they been standing.

At the boards, they were standing,

But much more interested in visiting with those in their group.  

Maybe it was just this group.

Maybe it was a call to revisit expectations.

Whatever the case, this is something easy that I can work on next year.  

Ch 5 Reflection - How We Answer Questions

I will be honest,

Some days my answering student questions is better than other days.

And it may depend on how much time was allotted for the problem.

The more time allotted for struggle, the better my questions.

I did see more keep-thinking questions as we went through the year.

Especially when it came to thin-slicing.

They always wanted another problem to try.

I also heard questions such as, "would this work with negative numbers?"

To try to keep students thinking my go-to questions centered around the following list.

"What do you think of this answer?"

"Why do you believe it is correct?"

"Will this always be true?"

I also did the walk away method quite often.

Or I would position myself in the middle of the room,

Simply watching and listening,

Before starting my rounds.

Things to remember for next year.

Respond to Is-It-Right-Questions with 

"Me telling you that it is right is worth almost nothing. 

If you can tell me that it is right, however, that is worth everything."

This is such an important piece of all the strategies,

That this short reflection is a surprise to me. 

However, with having a discovery classroom prior to this,

This type of questioning students was already in place. 

By having six whiteboards going, 

The questions I asked were more specific to each small group,

Essentially moving thinking even farther.  

Ch. 4 Furniture Arrangement Reflection

This will be a short reflection

As not much changed in my classroom based on this chapter.

I already had 4 tables that seat four students per table,

And two tall tables for two students each. 

With a whiteboard on the east wall 

And a large TV on the south wall,

There really was no front to the classroom to begin with.

My desk is in the back corner of the room.

Although I do have a table in the front corner where the document camera sits,

It's usually just used to hold materials and handouts needed for the lesson.

When something is needed to be projected,

Then the focus turns to the "front" part of the room.

I use a seating chart so students have a home base when entering the classroom.

These table groups are used when we don't have random groups at the boards.

This also helps when I have a sub teaching my classes.

One of my thoughts though is I could switch up the table groups as well 

For days when we aren't at the boards.

With the boards, I do find myself moving around the room 

when bringing the group back together for whole group discussion.

With the rich math on the vertical white boards,

Attention is directed to various methods of solving the same problem,

Misconceptions and questions from the group.

We have also used what's on the boards to help clarify our rough draft thinking

As we try to figure out what a particular group was thinking of trying.

Ch. 3 Reflection: Where Students Work

Let me just summarize this up quickly.

Vertical white boards have changed my teaching.

Vertical white boards have increased the amount of thinking in my classroom.

Vertical white boards have made math accessible to everyone.

Vertical white boards have helped students develop a growth mindset.

Vertical white boards made learning fun!

In fact, I had one class who would ask every single day..."Boards today?"

And when my answer was YES, the students would cheer.

Yes. 

You read that right.

They would cheer to do math.

Markers was the one thing that we struggled with.

We went through A LOT of markers.

Markers seemed to walk off at times to other boards.

Next year, I will make a greater effort to allow only one marker per board.

To help with this, I bought broom holders that I will attach to the boards.

Another change we will be making next year 

To help with our functions and graphing unit,

Will be to attach large sheets of laminated graph paper to the boards.

This way, students can complete problems 

And everyone can see their work.

Speaking of seeing the work on other boards,

This developed into a useful tool as time progressed.

We started the year with conversations of how valuable it was 

to look at all the boards when solving a problem.

At first students felt like they were cheating.

But as we progressed through problems

They started to realize how useful the other boards could be to get unstuck.

Any idea...even an idea that isn't correct,

Could be the catalyst of correctly finding a solution to the problem. 

Thinking also was increased with viewing others' boards.

As work and possible solutions were compared,

Students had to think through their thinking to justify their solution.

When asked about using the vertical white boards in their math learning, 

here's what the students had to say.

The best part of working at the boards...

"After working on a problem we get to discuss what we did."

"The best part about boards is it is 2 or 3 brains thinking instead of just one."

"It's not as boring, because you can discuss what you're doing with your partner and pick how to approach it rather than having to do it one way."

"Getting to see what other people are thinking."

"As you call it when you have 'ohhhh' moment and understand."

"That's usually when I learn the most."

"You get to see things from other people's perspective and you get to hear and see how to do things differently."

"You get to watch other people do math and see people do math different than you so you learn how to do some new math."

What is not liked about working at the boards...

"You can get paired with people that don't want to talk so it's hard communicating."

"Getting partners that don't want to work."

"The teacher couldn't be at everyone's whiteboard."

"I didn't like everyone looking at my board when I didn't know what I was doing."

"The time limit. I think it's better to have a little bit more time to solve or check the problem."

"Feeling rushed."

How did the boards help (or hinder) your math learning...

"They help because I can see where I went wrong by looking at other boards."

"The boards help me because it lets me picture the problem better."

"You can get rid of mistakes easily."

"They help us put our information down instead of just trying to keep track of it in our heads."

"It helps when you get feedback from others to see if you did it right."

"It helped by changing the way I look at math."

(Whoa.  That's huge.)

When a problem was solved at the boards, how did you feel?

"Awesome...like I accomplished something."

"It makes me feel great and I want to do another one."

"It made me really excited and made me feel good like I can actually do something."

"It makes me feel like I conquered the math problem."

"It made me feel good and want to try to keep solving math problems."

"It made me feel good and confident about the next one."

One of the true tests of this is when students that rarely engage

Are seen up at the boards working away.  

My principal, on more than one occasion,

Has walked in my room and was surprised to see so-and-so totally engaged.

Now that is a testament of the power of where students work.

Ch. 2 Grouping Reflection

We started the year creating random groups by handing out playing cards.  

This worked pretty well.

I would adjust the cards for every class.

But I soon tired of handing out and then collecting them all again.

While it probably only took a minute,

It was too much time being non-productive in my eyes!

Surprisingly, we never lost a card!

If I were to use cards in the future,

I would stick a library card pocket on every board for the cards,

Making collecting them easier as I move around the room.

We switched to the app Team Shake.

I had read about this app on the Building Thinking Classrooms Facebook group.

What a quick way to create truly random groups!

Plus, I could discreetly shake my phone to create a new set of groups 

if I happened to notice a pairing that wouldn't work that day.

We never had more than three at a board.

And even then, this sometimes was too many

As the third participant would sometimes take the passive seat in the learning process.

A couple hurdles that we had to get over with random groups was

1) the concept of being kind to others, even if you don't want to be in their group

2) not wandering to other groups to talk to friends

When these things happened, we would revisit the group expectations

and the importance of being kind and being able to work with others.  

Students reported on the reflection survey their thoughts about the random groups.

"I like them because it shows you different people and their struggles with the problems so you can help them."

"I felt like I just got partners that didn't do anything or people I just didn't get along with."

"It depended on who you are working with for it to be a good learning experience."

"[Random groups] were good because I could get help or my team could get help."

"Random groups are better so we don't just choose our friends."

"It was great because you didn't have the same people all the time."

"It would help us know more about each other and it helps cause it's a different person trying to explain it if you don't get it."

"I liked it because you got to share info with people you've never met before."

"It was nice because not only did you get to see how other people learn, it really helps you learn how to work with others."

"I disliked random groups because I would get people that would mess around."

I will continue to incorporate random groups next year.

To help with working with and getting to know others, we might need to use more 

  1) Kagen Cooperative structures and 

  2) Get to know you activities at the beginning of the year.

This might also need to be repeated when classes switch for the second semester. 

I might also incorporate a peer rubric of sorts.

(Was this mentioned in a following chapter?)

The rubric would help students remember the expectations when working at the boards.

Just off the top of my head right now...

--> Contributes their thinking/ideas

--> Asks questions of the group

--> Utilizes the marker when it's their turn

--> Stays engaged at the group's board

--> Respects those in the group

Students could rate themselves and also rate the peers in their group.

For each expectation, students would assign a number.

       2 -- Expectations were met on a consistent basis

       1 -- Some expectations were met and some need work

       0 -- Most expectations were not met 

I would not use this as a grade, but as a tool for growth.

After collecting data for a week/month, I would share averaged scores with each student. 

Chapter 1 Student Reflection: Types of Tasks

Four sentences in Chapter 1 grabbed my attention the first time I read the book.

"Students will get stuck.

They will think. 

And they will get unstuck.

And when they do, they will learn --

they will learn about mathematics, 

they will learn about themselves,

And they will learn how to think."

In my end-of-the-year survey,

I wanted to see how students perceived their own thinking.

I was seeing waaaaay more thinking than from years past.

But what were they seeing?

How were they reflecting on their learning?

I was pleasantly surprised to see that students were seeing their learning in the same way I was.

For them to be aware that they were thinking through the math problems,

Then they were probably aware that they were learning these very math concepts.

Which was another question on the survey.  :)

For 64% of my students to feel like their learning was greater than in years past,

Was proof that the vertical white boards were being seen as a valued tool

in the thinking, and ultimately, learning process.

When students explained their thinking for their overall learning,

I was blown away by their answers!

"It was greater because I was more focused."

"I'm getting good scores from my quizzes and I'm understanding problems better."

"I learned more standards than I have in previous years."

"There were different ways of learning how to do something"

"Last year and the years before, I really struggled with keeping up and understanding mat.  It was my hardest subject. But this year I really started understanding and enjoyed doing the math and gained confidence."

"Math is my worst subject but I am definitely doing better at it now."

"I never really picked up math this well until this year."

"I feel like I'm not the best at math but I do feel like I'm getting better."

"I can remember what we did at the beginning."

"I feel like learned quite a bit this year, because I paid more attention."

"You filled some of the gaps [in my learning] that I needed filled."

 

When asked what strategies they [the students] relied on when they got stuck...

"I just restarted and tried different ways."

"I looked at the other boards to see how they were solving it."

"I would THINK about what we did in the classroom."

"I would talk about it to find what was wrong."

"I would look [through my work] from the beginning for any faults and skim through until I got to the part we messed up on."

"Ask other people for how they understood the problem."

"I would try to find another way to solve it."

"I would ask for help."

While this data and the many comments do not simply address the Type of Tasks that Chapter 1 addresses,

This data is in direct response to the three sentences that started this whole journey.

I wanted to increase mathematical thinking in my classroom.

And from what I've shown here,

I believe that happened.

When the Math Teacher Teaches Reading...

My students have struggled reading all year long.

I believe they can read, 

But they just don't like it.

I have worked really hard to get good, interesting books into their hands.

And this has helped.

Somewhat.

As a reader myself, this "inability" to read for 30 minutes at a time

Has been a thorn in my side all year long.

Students need to be able to read.

Students need to be able to read for longer periods of time.

Students need to understand what they are reading.

Maybe this is the problem???

Soooo...once library books were due back in for inventory,

I had to find something to fill the time.

Why not go over reading strategies one last time before high school?

With copies of Leonhard Euler in hand,

And a blank piece of typing paper in the other,

We started reading.

Outloud.

Paragraph by paragraph.

Stopping at predetermined various points.

Our focus was going to be on practicing what good reading looks like.

We first paused to draw a visual from the Biographical Information.

They could pick any point that a picture had popped into their head while we were reading.

We took a little time to discuss the pictures 

and how they were similar and different than others in the class.

Our next stop was in the Contributions section of the reading.

A mathematical concept was described,

One I knew my students could identify with,

And I wanted to see if they could picture it.

It involved labeling a triangle's sides and angles.

This was very eye opening as I saw connections being made to Pythagorean's Theorem!

Another stop was also in the Contributions section.

It had mentioned pi and how Euler was responsible for this symbol.

Students had to write about what this section made them think of.

Another opportunity to connect to their mathematical learning this year.

Finally, we got to the Quotation.

"He calculated just as men breathe, as eagles sustain themselves in the air." ~ Francois Arago

We dove deeper to figure out what the author was trying to say here.

The responses were amazing!

"He was always doing math, like it came natural to him."

"He did work easily and he worked all the time."

"Breathing is easy so he is saying that's how easy math is for him."

Today, as we finish up the piece,

We are going to focus on the following areas.

1) Write one or two sentences to summarize what you read in the Anecdote Section.

2) What thoughts do you have when Euler had to settle the argument between two of his students?

3) Can you picture all the places Euler taught?  (Look at a map to get a better understanding of the area he worked in)

4) After reading three sections: The Pillaged Farm, The St. Petersburg Fire and The Smart Pencil, connect character traits of those in the writing with our pillars (respect, responsibility and growth mindset).  Where do you see each of these?

5) Finally, in the Birth of Topology section, Euler creates his own visual of a real life math problem.  How does his drawing connect to the real life situation?

Measuring Growth

State assessment scores came out yesterday.

This was the day I had been eagerly anticipating. 

I couldn't wait to see how the use of vertical white boards

Impacted learning in my classroom!

As my eyes scanned through the scores,

Searching for my data,

My heart plummeted.

We had scored below the state average.

The high hopes I had to see an increase in learning

Just wasn't meant to be.

What could I have done differently in my teaching?

What gaps still exist?

Should I have used a more traditional approach of instructing?

Would incorporating homework again be the fix all?

What would the scores have been had I NOT implemented the Thinking Strategies 

as outlined in Building Thinking Classrooms?

As I crawled out of the pit of disappointment,

I realized that the state assessment is just one snapshot of my student's learning.

Growth was shown by our daily Test Trainer (MidSchool Math math curriculum).

While I would have liked to have seen more growth,

(What teacher wouldn't???)

I couldn't ignore the fact that growth was evident.

I also checked our Fastbridge scores.

Again, the students showed growth.

My take away from all this?

Change takes time.

There is more than one way to measure success.

Look for the positive in all things.

Student Reflections - What Life Lesson Did you Learn in Math Class this Year?

One of my learning goals does not even center around math.

I want my students to walk out of my classroom 

more prepared to be a productive addition to our community outside these four walls.

I always ask at the end of the year,

What life lesson did you learn in math class this year?

This year's responses literally made me tear up.

Is it because of the climate change in our classroom with vertical white boards?

Is it a post-COVID thing?

Is it this group of students?

Whatever it is, this teacher's heart is all warm and fuzzy right now!

"Mistakes are okay."

"To discuss stuff to other people to understand it better."

"To not look at something and say it is too hard."

"That you will have to work with people you don't like."

"Don't ever give up."

I"t is ok to fail but not give up."

"If I try hard and give it my all I can be smarter than I ever though I was."

 

"That life is just a learning lesson."

"Everything has an equation!"  (LOL!)

"Things don't always go the way you plan."

"To use information wisely and to learn from your mistakes."

"Everyone has their strengths and weaknesses."

"Not everything comes easy."

"Things may seem hard because you don't want to do it, but they can actually be fun."

"There is always more than one to fix a problem."

"There are multiple ways to solve math problems and there are multiple ways to solve life problems and many ways work so you should always listen to everyone's ideas."

"It takes respect to gain respect."

 

Don't mind me...I'm just over here tearing up a bit.

BTC Chapter 1 Reflection: Types of Tasks

The end of the year just begs for reflection.

And after implementing Thinking Classrooms,

The list of changes and what went well keep swirling in my mind.

So to organize my thinking, 

I plan to reflect on each chapter. 

Soooooo....

Let's start with Chapter 1: What Types of Tasks We Use in a Thinking Classroom

What Went Well (with changes in red)

It is imperative to start with non-curricular tasks to set up the expectations of VWBs (Vertical White Boards).  We started with the Painted Cube problem the very first day.  While it was a good problem and tied in nicely to upcoming 8th grade standards, I might switch it out next year.  The Tax Collector problem is a good one to get conversation going at a level everyone feels comfortable in.

We also did the problem finding solutions for 1-20 with only four fours.  This was excellent to review the order of operations in a non-traditional type lesson.  

We did the Palindrom problem.  The students really got into this.  I would like to dive deeper into this problem so see where it can go.  

Lastly, we completed the Locker Problem which was also a good one.  

Our first attempt at using curricular tasks was when we reviewed operations with integers.  I used a missing number puzzle to really emerge them into thinking about what happens with adding and subtracting negative numbers.  Once I got to understanding thin-slicing problems better as the year progressed, this would have been an excellent way to extend thinking and get more practice in.

The non-curricular tasks definitely did their job in propelling students to WANT to think.  Many times, especially here at the end of the year when I threw a couple of non-curricular tasks at them, the students DID NOT WANT TO STOP for the discussion piece.  They wanted to KEEP THINKING!!!  This was my entire reason for moving to a Building Thinking Classrooms approach.  I wanted more thinking happening in my classroom!

Things to Think About for Next Year

I need to get better at extending the problem.  For example, in the Tax Collector problem once they figured out they could beat the Tax Collector, we then moved on to the question: What is the largest amount you could make?  After they figured that out, we extended it to 24 paychecks.  

Do I still continue the Simulation Trainer lessons from MidSchool Math, when all they are is essentially mimicking a task??? At this point, I believe that I can continue to use this component of the curriculum if I make a valiant attempt to push their thinking and fluency afterwards.  This can be ONE problem that extends the learning.  Or it can be the Check Your Understanding (Practice Printable).  But my goal will be that if the Simulation Trainer is used, we spend more time on a rigorous problem(s) afterwards.  

That Successful Feeling!

Yesterday we did another problem at the VWBs.

It had been a while. 

We had to review expectations,

And talk to why some were harder to follow at this time of year!

(End of the year attitudes are a tough hurdle to get over!)

Since we had been learning about volume before the state assessments,

The task was to find the remaining volume in a cylinder after a cone with the same diameter and height was placed in the cylinder.

I only gave them the slant length and diameter.

Only about 1-2 groups were able to work through the problem.

And this was even AFTER we would pause for some rough draft thinking aloud as a whole class!

I asked a few of the students that were successful on their own solving the problem,

How they felt after completion of the task.

Their responses are below.

The students responding to their success only included one high achieving student.  

The other two have struggled in math.

"Knowing that I can make mistakes while solving problems takes most of the pressure off so you aren't thinking that you have to get it right and if you mess up you can't change it."

"When completing a problem in math, it's exciting and makes you feel like something you did is good.  It makes you feel relieved and like you just won 100,000 bucks!"

"I feel great and it's exciting.  It's fun when you understand what's going on in the problem."

When You Change the Way You Grade...

When you change the way you grade,

You might be paving the way for more learning.

This year, I took away grading any and all classwork.

I no longer gave homework that was required.

Answer keys were always posted on Check Your Understanding days.

Some days students completed a LOT of problems.

Some days, very few.

But every day our goal was the same,

To move our thinking.

With the implementation of Vertical White Boards, (book Building Thinking Classrooms)

And Rough Draft Thinking (book, Rough Draft Math)

Students were more focused on the math content

Then on just getting the problems completed.

When the goal is just to complete something,

Then we've lost focus

on meaning-making,

and using the content to move our thinking.

Just the other day, out of the blue,

One class announced how they liked this grading system better than other classrooms.

I was shocked.

It's a much harder way to earn a good grade

With only quizzes and individual work counting.

But by doing this,

A more accurate picture is being drawn on what the student knows.

The grade is no longer how responsible the student is in getting work completed,

It no longer reflects classroom participation,

It is a true measure of their learning.

To support this evidence,

I counted the number of semester F's for this year, 2021-2022.

I also went back several years,

Back to a time where I gave a grade for completion,

Where classroom activities resulted in participation grades.

And remember the Covid Year, 2020-2021?

(Who could forget that year...hybrid this, remote that...it was crazy!)

To keep a better track of my students progress in the learning activities,

Absolutely everything posted to Google Classroom got a grade of some sort.

Check out the number of F's that year!

In summary, I will continue with this grading system into next year.

Is it a fluke and only worked with this group of students?

Is it legit and really is the best way to enhance learning in the math classroom?

By taking away the grade, does learning really increase?

Can't wait for the state assessment scores to if that's the case.  

Fingers. Crossed.

Visualization in Math to Increase Comprehension

We are working on our reading strategies.

And it's been easier to implement in the math classroom than I initially had thought!

Upon our return to school after spring break,

We reviewed the quiz on functions we had taken before we all went our separate ways for a week.

To do this, the students first analyzed where their strengths and weaknesses were.

Using the chart below from BTC, 

Students made notations to find any patterns.

While I was focusing on the horizontal rows of content,

I was surprised when a student piped up that he had mainly checkmarks in the Basic column,

But that he was missing most of the Intermediate and Advanced problems.

Interesting.

For me. 

As his teacher.

While it's important to start at the concrete, basic level,

This was a red flag for me to continue to push them to a higher level of rigor and increase in fluency.

At this point, I started in on how they visualized certain vocabulary words and statements.

We started with the word "Function".

What did they see in their mind when they read the word "function".

After all of my classes, 

I had a much clearer picture of what they were seeing when they encountered the word, function.

We discussed each visualization after they drew them up on the board. 

We again pointed out similarities.

We asked for justifications.

We found mistakes or misconceptions to revise the picture and ultimately, the understanding.

We did this again for the concept of proportional relationships.  

I loved how in each case,

All three representations were included!

I was expecting the graphs,

But not the equations, with them being the most abstract. 

One of the best realizations of this activity,

Was noting how many students do not have a picture in their mind 

when they encounter these vocab words.

My hope is that when students shared their images,

And our discussion followed,

That they students were able to now attach a visual to the word. 

Selecting Tasks - Chapter 3 Rough Draft Math

We had a field trip to an area technical school today.

On the way, I read chapter 3 in the book, Rough Draft Math. 

It was all about selecting tasks that invite rough draft thinking.

• Tasks that ask students to explain their thinking
• Tasks that have more than one good answer
• Tasks that can be solved with more than one good strategy
• Tasks that ask students to predict and then test and revise problems

While on the tour, a student pointed out one of the whiteboards with all the math on it.

As we left the room, he said, "I think I recognize some of that math on there!"

I quickly ran back, took a photo, and forgot about it until we got back on the bus.

Sure enough!  There was math that my 8th graders would recognize!

I cropped the two pieces that I wanted to focus on,

And for the remaining two classes of the day,

We dove right in to seeing what we noticed or wondered about the problem.

We didn't have any context to go by,

But we could make connections to what we had learned,

And then make predictions to what we thought they might have been learning about.

We had just been learning about linear functions,

And the students immediately recognized that the students at WSU Tech had been solving for y.

My next question was, is y = x/5 a linear function?

Their choice of how to solve it was to create a table and pick the inputs.

They quickly found the pattern and we were able to graph it to confirm it was linear.

I then switched it around to y = 5/x. 

Just wondering outloud how that might change things.

This turned out to be a great intro to our lesson tomorrow, linear vs non-linear functions.

We then moved on to the next problem.  

I started this discussion the same way, "What do you notice?"

"Does this remind you of anything?"

"What do you think they are trying to solve?"

The discussion was great!

It started off slow.

"I see a square root sign."

"They changed the fractions to decimals."

"Why are they squaring the decimals?"

And then pretty soon, they connected it to the right triangle,

And the connection to Pythagorean's Theorem was made!

As a class, we then explored why it was written as it was.

This was most definitely not how we had been solving for missing side lengths!

What a great follow up discussion to a great tour!

What great examples of where the things we are learning will be used!

What a great review of grade level content!

Learning Retention

So this year I've gotten my students thinking more.

Plus, we are using rough draft thinking as a stepping stone in our learning,

But when I measure what my students are retaining from all our learning,

We are not where we need to be yet.

I shared this data with my students last week.

We noticed that the fall scores (blue bars) tended towards the upper percentages.

While the spring scores (red bars) tended towards the lower percentages.

When I asked students what this meant,

The looks on their faces said it all.

They weren't remembering what they were learning!

Today, we looked at just their retention during the Functions unit.

This is a large unit covering the five function standards, slope, and proportional relationships.

And we still have more to go...non-linear functions and bivariate data.

The data is showing the same slipping of holding on to this new learning.

So I started researching.

I'm including these websites to reference when I have time.

But will continue looking for more strategies to help my students.

1) https://mathsnoproblem.com/blog/teaching-practice/7-maths-mastery-strategies-to-retain-knowledge/

May need to focus on the revisiting part.  While test trainer revisits all the concepts in a spiral, there is no reteaching during this unless a student looks it up.

Would be interesting to compare McCurdy's students average with the non-McCurdy students to see if more exposure is helping.

2) https://mathsnoproblem.com/blog/teaching-practice/helping-learners-retain-knowledge/?utm_source=blog&utm_medium=blogintlink&utm_campaign=7strategiestohelplearnersretain

Focusing on the forgetting curve and the ideas suggested in this article.

Also, focusing on mastery. https://thirdspacelearning.com/blog/what-is-maths-mastery-teaching/

Choppy and Sloppy Talk - Chapter 2 Building a Culture

Two terms have emerged as go-to's in our math class this week.

When trying to explain our thinking on a problem,

We are noticing that when trying to make sense of something,

The words are not always there.

What comes out is choppy.

Sloppy.

Sloppy and choppy even happens to teachers that get stumped.

Which I think it a very valuable learning tool,

When students can see their teacher struggle to make sense of something.

On Monday, I had asked the students to justify if all three functions were indeed linear.

They could not simply say they were or they weren't.

They had to show evidence of how they knew on the vertical white boards.

On one board, it was brought to my attention, that a student was dabbling in both y- and x- intercepts!

Whoa.

Didn't see that one coming.

So I jumped on board, brought everyone's attention to his board, and started in.

Halfway through, as we worked through justifying the new thinking he brought to the discussion,

I started to notice something wasn't working as it should.

His "new" math idea wasn't jiving with all our work prior to this.

I started to stumble in my thinking,

My words coming out sloppy and choppy

As my brain was in overdrive to figure out where the mistake was.

Why wasn't this working.

The surprising thing was, 

I. Did. Not. Panic.

The first thing I noticed,

Was that the students were practically in my lap.

They had all pressed in to be closer to the board in my struggle.

They were asking clarifying questions.

Our roles had switched.

They weren't understanding the problem either,

But were trying to help ME understand it!!!

The active learning that was taking place was amazing!

Rough. Draft. Thinking.

Allowing ourselves to be vulnerable in the learning process.

A place where we just talk to learn.

I also noticed the benefits of rough draft thinking with one particular student last week.

This student, prior to last week, had been disengaged in the learning process.

Rarely turning to look at the board that was being discussed.

But for some reason, after I talked about this new book I was reading,

And that I was encouraged, because we were already doing what it was suggesting,

He seemed to find courage in talking through his learning.

In fact, every time I came around to his group,

He would engage me in what he was thinking,

How he was thinking.

After about two days of this new behavior,

I watched him walk out of math class with much more confidence than I had seen from him in the past.

My takeaway...

It's important to teach students the content.

But it's also important to teach students how they learn.

By instructing them on these strategies,

They can see for themselves, when implemented, how much these new found tools do help!

Tying in Vocabulary

Students reported that the review of math vocabulary is important to understanding the question.

This was brought to light on Monday when the words "initial value" was used in place of "y-intercept".

Today, while students created graphs, equations, and tables for three space ships in a race,

I had them write their statement using as many of the following vocabulary words that they could.

function

linear

slope

rate of change

y-intercept

initial value

proportional

Here is an example of one student's work.

"Spaceship #3 will win. The slope of the function is greater than the other linear proportional functions. It makes it proportional because the initial, or y-intercept, is 0."

Rough Draft Math Book

I'm starting a new book.

Rough Draft Math by Amanda Jansen.

I saw somewhere that this book is a good choice to follow Building Thinking Classrooms.

I'm one chapter in, 

And I believe I have made a good choice!

Some highlights...

"By expressing ourselves, we learn more..."

"getting into the conversation, helps you understand..."

"participating in math class is an opportunity to continue learning, not an obligation to perform..."

"When we learn, we actively work to make sense of an idea that does not make sense to us yet."

"Our use of bumpy language is actually productive struggle in action."

"Rough draft thinking sounds like communicating what we notice, explaining why something does or does not make sense initially, trying on a new way of seeing a relationship, or making new connections and articulating them".

This first chapter brought to mind several things that happened in my classroom this week.

Rough Draft Math might not be so hard to implement as the next step. 

Scenario #1

While reviewing slope, one of my questions referred to parallel slopes.

A couple questions later, it focused on a slope less steep that y=1/2x+8.

A student suggested using -2 as the new slope.

After graphing the two slopes,

A student just blurted out, "Those lines look like they cross at a 90 degree angle."

This prompted a discussion on what the mathematical vocabulary is for two lines that intersect at 90 degrees.

Which then moved the discussion forward to a place I had never anticipated going...

Teaching what slopes make perpendicular lines.

I wrote on the board that a line with a slope of 1/2 is perpendicular to a line with a slope of -2.

I then made a quick decision to offer some thin-slicing problems to see if students could make sense

of what slopes make perpendicular!

Students quickly talked through the first couple of problems,

If a line has a slope of 1/3, the slope of a line perpendicular to it would be ____

If a line has a slope of 1/4, the slope of a line perpendicular to it would be ____

I then asked if they could put into words what they saw was happening.

Many students yelled out, "Keep Change Flip!"

I could see why they said this, they were seeing fractions flippling and the sign was switching from positive to negative in the examples I had given.

With several wondering question from myself,

"What are these fractions called when the numerator switches places with the denominator?"

"What do you mean by 'change'?"

"What's a better word for when a number goes from positive to negative?"

And pretty soon we got it summarized that perpendicular lines have slopes that are opposite reciprocals.

"participating in math class is an opportunity to continue learning, not an obligation to perform..."

"getting into the conversation, helps you understand..."

I had students in the conversation that rarely jump in.

Some students were leaning forward in anticipation of figuring this out.

It was one of those moments in math where you just let the conversation take over.

Scenario #2

"Rough draft thinking sounds like communicating what we notice, explaining why something does or does not make sense initially, trying on a new way of seeing a relationship, or making new connections and articulating them".

On 2/22/22 students could choose from two activities...

One activity was working with fractions.

They had to make all the problems equal to 2.

It was eye-opening for me to see their number sense and how they thought and worked with fractions.

Of course, dividing fractions, seemed to be the biggest stumbling block.

As I listened to students trying to make sense of these problems,

I wondered how we could make this process easier with pictures.

After deciding to go with the concept of pizzas,

We talked through it together as a class, myself included,

How to visualize these problems to figure out how to get the solution of 2.

Ironically, while typing this, I now have noticed another relationship that would have made this so much easier.

We could easily have just divided it by two to find the divisor we needed!  

An example of where there wasn't enough time to finish the conversation!

"When we learn, we actively work to make sense of an idea that does not make sense to us yet."

When Students Take Notes for Their Future Forgetful Self

So this happened today.

A student created review notes.

On her own.

On her own time.

At home.

To make sure she got the main points from that day's lesson.

Wow.

Now if only all my students would see the benefit of this!  

When Everything Falls Into Place

Today we started with a short thin-slicing review.

I gave the students the equation y=1/2x + 8 and everyone had a white board.

The first task was to write an equation parallel to this equation.

The second task, an equation steeper than this equation.

For those few students that put a fraction for the slope that was less than 1/2,

I simply stated that their equation was not steeper than mine.

They sat there stumped.

I assured them that this mistake was one that would help them down the road.

Which got the attention of other students,

Who now wanted to learn from a mistake!

The third task, the one where I would see how deep their understanding really was,

was to write an equation that was less steep.

I knew that I would see negative numbers pop up as the slope.

And this was one of my goals of our review,

To uncover a misconception and unravel it.

To my surprise, only one student in each class put down a negative number for the slope!

I was expecting so many more.

Also to my surprise, students were showing fractional understanding 

As the fractions they were using were mostly less than 1/2.

Wow!

After summarizing what kind of slopes would be less steep.

We dove into the negative slope.

Many students thought that since a negative is less than 1/2 numerically,

As the slope it would have to be less steep.

Another surprise that came out of the lesson

was being able to push their thinking towards what makes perpendicular lines.

When the slope of -2 was given,

We were able to use comparison strategies to figure out what slope makes a line perpendicular to another line.

Score! 

We just moved our thinking to the high school level!

Thin slicing.

Whole group discussions.

Mistakes.

When all mixed together, make a great learning experience!

Thin Slicing As A Way of Life

Once I started focusing on thin-slicing,

Both the students and I have been enjoying the challenge.

We are in our function unit,

Learning about y=mx+b.

Yesterday, we did a series of problems for writing equations in slope intercept form

From just a point and the slope.

We started off easy.

Slope = 3, (2, 4)

Students were using graphs and tables to figure out the equation.

We reviewed how graphs are the most concrete,

How they help us visualize the line and make finding the equation very easy.

I then introduced the most abstract method,

Using the equation and plugging in the pieces.

Now students have three tools in their toolbox - graphs, tables, and equations!

My next problem was a little more difficult

With the slope = -3 and going through the point (4,1)

While some students still kept with the graph or the table,

Many tried the equation method and found the efficiency of using this method!

And at this point, 

As students found success and understanding,

More often than not,

They would ask for a harder problem!  :)

Vertical White Boards (VWBs) Increase Individualized Instruction

So here's what I've noticed 

That I LOVE about using my vertical white boards.

The individualized instruction has totally INCREASED!!!

As I meander around the room,

I am able to address each group's individual misguided thinking.  :)

Making their instruction personalized and timely.

In the past, I would try to address these things with the whole class.

This was rarely as effective as I was hoping.

Not every student needed this additional instruction.

Off task behavior would start to surface.

Plus, the very student(s) that needed this reteaching

Might disengage as the whole group was made aware of this gap in knowledge.

Now, as clarification, if I see the same misunderstanding board after board after board,

At that point, it might be best to address the whole group in the sake of time.

Using their boards as a springboard for the discussion,

Everyone has an iron in the fire for moving their thinking.

This is usually VERY effective for unsticking the stuck groups.

Let's go back to individualizing instruction

And the example that played out in my room yesterday.

The 8th grade standard we were working on was calculating slope.

As I walked my room,

I was finding hurdles that would stop my kids in their tracks.

First, students didn't know how to graph coordinate points.

This totally derailed the concept of checking their work.

So...a quick mini tour of the coordinate grid system was in order.

Second, I was noticing students struggling with subtracting negative numbers.

As this was something I anticipated already in August,

I was surprised that after our teaching at the beginning of the year

The concept was still not being able to be applied with mastery.

Ok.

Nevermind.

I wasn't too surprised.

Students have struggled with subtracting negative numbers since the beginning of time.

But I was disappointed that all our efforts to battle this in August,

Didn't work.

More work is needed.

And another stumbling block popped up with just a handful of students.

Equivalent fractions.

Students were finding the slopes

But if they got 4/8, they were not recognizing it was the same thing as 1/2.

No wonder I was tired by the end of the day!

Not only was our focus on slope,

But I was making decision after decision how to effectively re-teach these concepts 

To help my students move around the gaps in their learning. 

With the quiz over slope today,

Our measuring stick at the end of the lesson was me asking,

"Where is your confidence factor knowing that you get to show me what you know tomorrow?"

For the students that applied themselves,

Reflected on what they didn't know,

And thought through my re-teaching efforts,

They reported higher confidence factors

Than the students who had not been engaged or reflective in their learning.

Thankfully, with how my Building Thinking Classroom is evolving,

This was not that many students.

Most students walked out more confident then they had walked in!

When the Class Moves the Discussion

As I create my math lesson each day,

I know where we are going with the content.

I also have a pretty good idea of where the struggle will happen.

I allow this struggle,

As the learning that follows is super rich.

But then there are days like today,

Where the magic happens.

Today the students took the lesson 

And went farther than I thought we could go in a day.

I didn't even suggest this route.

I just watched it all unfold on the boards.

The lesson started out with me giving them two points.  (9,6) and (3,5).

We had discovered the formula for how to find slope the day before.

Today we were going to thin-slice the concept, starting with positive whole numbers and positive slopes,

Before moving to negative numbers and negative slopes.

However, with just this one problem, 

I could see quickly as one group collaborated around board #3,

That my lesson was going to take a different perspective.

My lesson was going to cover not only how to find slope,

But where that slope is found in a table of values.

How fractions work in a table of values,

Simplifying fractions,

Adding fractions,

How fractions work in y=mx+b,

And how these points are on the graph.

So many connections.

So many relationships.

So much new learning.

So much review of concepts needed to minimize gaps.  

One problem.

One group of students thinking.

One lesson made better by genuine engagement.

When You Just Have 5 Minutes for Thin-Slicing...Take It!

So today we were using Anchor Charts

As a way to help students take notes for their future forgetful self.  

For the last couple weeks students had been using the concepts of slope and y-intercept,

Without even knowing these terms.

We had been referring to them as speed and starting points.

Today was the day we made the bridge over to the correct mathematical vocabulary!

Using only student input, 

We completed the charts to connect our previous learning to a more abstract way of thinking of functions.

In one of my classes, we had a little extra time on our hands,

Enter...thin-slicing.

As a whole group.

I put up a table of values, starting with x at 0 and asked for the equation.

It didn't take them long,

So the next table I created, did not start at 0.

Didn't stump them.

Then I gave only three points, with gaps in between.

Ummm...a little more stumbling, but they got it! 

Finally, I gave them only two points.

This got them at first, but then their learning started to kick in,

And eventually some were able to write it in slope-intercept form.

It was at this point, that I realized that Monday's lesson might be a little too easy for this class,

Based on what I was seeing.

I told the class this.

That I was going to have to make my next lesson more challenging.

What happened next was NOT what I was expecting.

I was expecting groans.

With exclamations of "NOOOO!!!!"

But instead,

The class cheered!

The. Class. Cheered.

They were excited.

Let that sink in.

They were excited for a challenge.

This Building Thinking Classrooms is the best thing since sliced bread in my books.

I absolutely love how my students are responding.

Because in their responses, I can see that they are thinking,

Connecting the dots,

And ultimately learning the material.  

Happy Weekend ya all!!!  :)